Draw a circle with radius 100

Challenge Level: Ready to expand

Learning outcomes

Students will be able to:

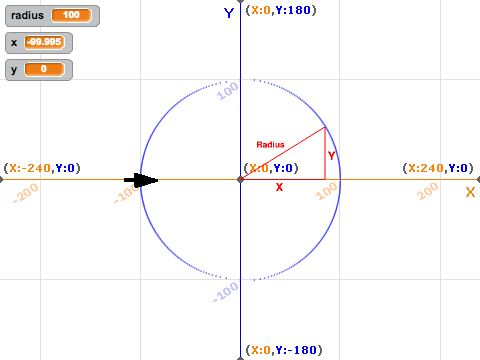
Describe how variables store values and how they are used in your program.
Computer Science: Programming
Describe how you have used mathematical operations in your program.
Computer Science: Programming
Explain how sequence works in programming.
Computer Science: Programming
Explain why a program gives the output that it does.
Computer Science: Programming

Requirement:

Write a program that draws a circle, with the given centre point x:0, y:0, and its radius equal to 100 steps. You can use the same method as the "Draw a 360-sided polygon" challenge, but this time you will need to work out how long each side is based on the circumference of the circle, and you'll need to work out the circumference from the radius.

Testing examples:

There are no testing examples for this challenge.

Languages

Scratch

What it should look like

Click on the green flag to see the expected output of your program.

View full screen

Recommended blocks

Hints

The radius of a circle is the distance of its centre to the edge of the circle.
The circumference is the distance around a circle (its perimeter) and is equal to $2 \pi r$ where $r$ is the radius of the circle.
To be able to draw the circle right in the centre, you will need to set your sprite to point in the right direction. To set the direction of the current sprite use the block under the “motion” script.

Show Scratch solution

Extra Challenge

Extra challenge #1: Write a program that works for any radius. That means that it takes a radius as the input then draws a circle with the given radius, and then displays the circumference as the output.

Extra challenge #2: Write a program that takes a circumference as the input then draws a circle with the given circumference and then displays the radius as the output.

Extra challenge #3: [This requires advanced maths, but is a good challenge for a student who is familiar with Pythagoras' theorem] Draw a Circle Using Pythagoras’ Theorem.

A red circle drawn using the Pythagoras' Theorem method.

The diagram above shows a circle (radius 100) drawn using the Pythagoras’ Theorem method. (Note: The red triangle inside the circle is only to show the calculation and does not need to be drawn).

You can use Pythagoras’ Theorem (in any right-angle triangle, the square of the side opposite the right angle is equal to the sum of the squares of the other two sides so here $x^{2}+y^{2}=radius^{2}$ ) to draw a circle. We can do this by rearranging the formula to solve for $y$ like this:

$y^{2} = radius ^{2} - x^{2} \\ y = sqrt{(radius^{2} - x^{2})}$

We then calculate $y$ using a range of values for $x$ (i.e. from 0 to $\pm radius$ ). Your programming language will probably only give you the positive square root, so you will also need to plot the negative of $y$ .