This lesson is primarily on a maths topic rather than Computational Thinking, but the modulo operator is so widely used in digital systems that we've provided this lesson plan to teach it explicitly rather than introduce it in each of the several topics that use it. The "mod" operation (short for modulo) is used a lot in the error correction and detection lessons; in the Unplugged activities it also comes up in searching (hashing), and it applies to angles in turtle based languages like Scratch and Logo. Students may already be familiar with the idea, since it is essentially the same as the "remainder" after division; it's also referred to as "clock arithmetic" because it is how we can add time.
The Modulo operator Unplugged
- Duration: 30 minutes
- Ages 8 to 10: Lesson 3
Printables
Classroom resources
- Counters
Programming challenges
Note from the authors
Key questions
- Which month comes first, January or December? What is the month after December?
- What is the weekday that comes after Friday? What is the weekday that is 4 days before Friday?
- If you arrive at a car park at 5pm (17:00 if you use 24 hour time), and pay for 8 hours of parking, when will it expire?
Potential answers could include:
- With the months, each month is both before and after every other month! If it's January, then there's a December just before it, but there's also one coming up in 11 months.
- With the days, again, Monday comes after Friday, but it's also before Friday.
- The car parking ticket expires at 1am (1:00). When you add 8 to 5 (or 17), you get 1!
Lesson starter
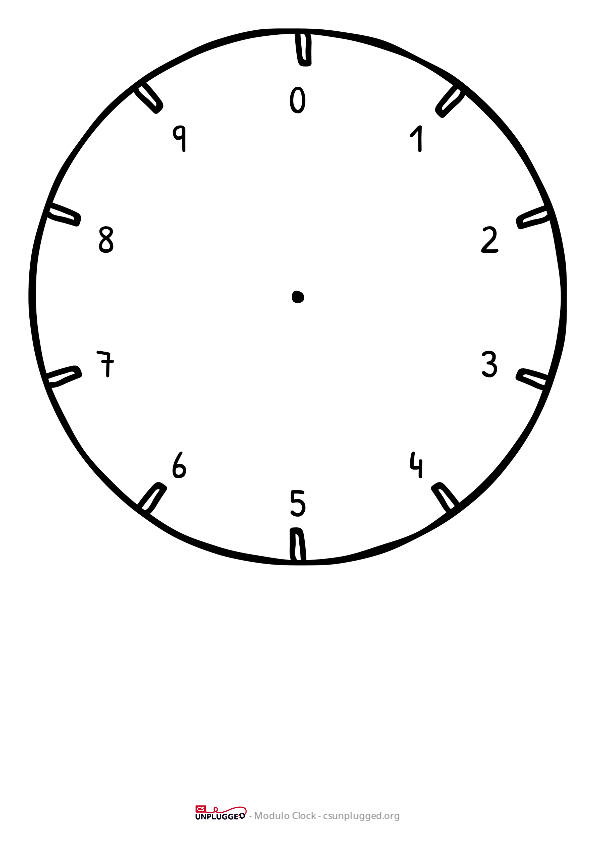
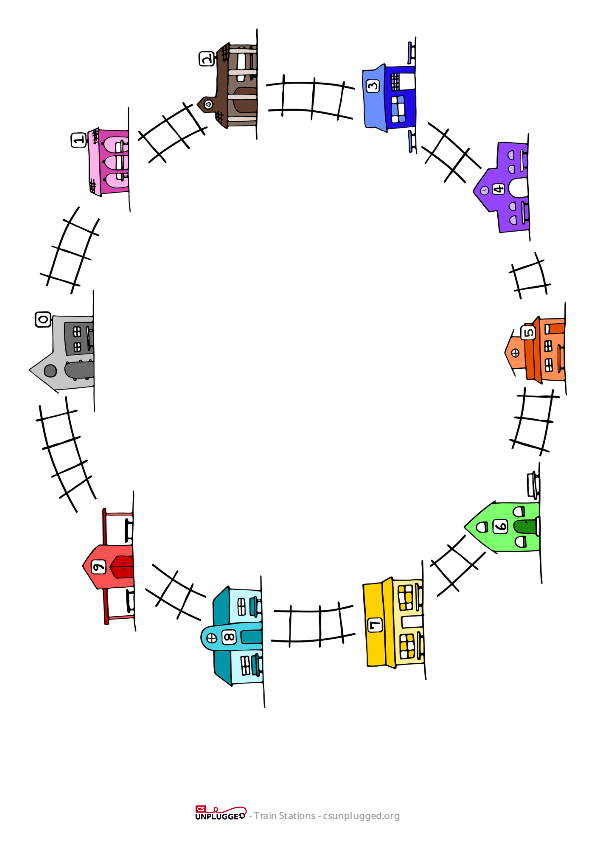
Print the modulo clock resource with modulo 10 out for the students, or draw it on the board (This sequence of questions could also be run using the train or ferris wheel model; see the next section).
Ask what is unusual about this "clock" (it has only 10 points on the dial, and it has 0 at the top instead of 10). Explain that although it's a little odd, it's actually very useful.
Lesson activities
Ask which number is 2 hours (or 2 ticks) after 3? (The answer is 5 i.e. just count 2 units clockwise). If students have their own copy of the clock, they could put a counter on the 3, and move it 2 places.
Which is 3 hours after 9? (2) We'll refer to this as 9+3.
What is 2+10 (i.e. 10 ticks after 2)? (It is 2, since adding 10 goes right around the clock). What is 2+20? (it's also 2; you go around the clock twice). What is 5+100? (5, since going a multiple of 10 gets you back to the same place).
Now compare the following sums on the clock with the normal sum:
- 8+3 (1, compared with 11).
- 9+8+7 (4, compared with 24).
- 6+6+6 (8, compared with 18).
Ask the students if they can see the pattern; with sufficient examples they will realise that it keeps the last digit of the sum e.g. the last digit of 11 is 1, of 24 is 4, and of 18 is 8. If they have done the product code activity, they may recognise this as the function that we use for working out the check digit in product codes.
The last calculation above is 3 times 6 (you could start at 0 and count 6 ticks 3 times).
Ask what 4 times 6 might be on the clock (it's 4, which is the last digit of 24). How about 8 times 5? (it's 0, since it's the same as the number 40).
This strange kind of clock arithmetic that we're doing has a name:
it's the modulo.
The clock here has 10 ticks on it, so the correct way to write
a calculation is: (8+3) modulo 10.
This means add the 8 and 3, but reset to zero every time you would have got to 10.
(This function is also called the "remainder" after division, which for positive numbers is the same as the modulo.)
Ferris wheels and train routes
The above exercise could also be done with the train or ferris wheel handouts, which also cycle every 10 steps. Students can use counters to track their movement around the stations. We have provided resources for train routes above.

Time to rewind
The modulo counting is like a circular number line. As well as going forward, let's experiment with going backwards (i.e. subtraction, or adding negative numbers). On the clock it would be winding the time back; on the train and ferris wheel it's going in reverse.
Ask the class what they think 2 - 4 is on this system (i.e. 4 steps before 2). (This takes you to location 8).
How about 2 - 10? (It's still 2). Or 2-100? (We're still going to end up at 2).
What is 0 - 7? (3)
But what about -8 i.e. negative 8? (That's 8 units before 0, which is 2.) Other numbers that land at 2 are -18, -28, and so on.
(This idea comes up with calculating some check digits; for several systems we need to ask "what do you add to x to get to 0 in modulo 10"; the short way to calculate that in a computer program is "(0-x) mod 10".)
Other sized clocks
Now have the students imagine (or draw) a clock with 11 ticks on it, numbered from 0 to 10.
What is 9+3 on this clock (it's 1).
What is 7+11? (7, since 11 goes right around the clock).
You can experiment with other sums, and other clock sizes. Modulo 11 is mentioned because it is used by ISBN-10 numbers.
If you get the students to consider modulo 12 or 24, they should see that it relates to normal clocks (12-hour or 24-hour clocks respectively). For example, (8+5) modulo 12 is the same as working out what the time is 5 hours after 8 o'clock; or (22+4) modulo 24 is the same as working out the time 4 hours after 22:00. In the modulo system, the number at the top of the clock would be 0 rather than 12 or 24, but all the other values work as expected.
An interesting one to experiment with is modulo 360 i.e. a clock with 360 ticks, numbered from 0 to 359. This kind of calculation happens when we add angles, since turning 360 degrees ends up in the same place as the starting position.
Have the students stand up and face the front. Now ask them to turn right 90 degrees (a right angle). Now have them turn another 90 degrees. Ask what angle they've turned in total (180 degrees).
Continuing on, have them turn 90 degrees twice more. They should now be facing the front. How far have they turned in total? (90+90+90+90 = 360 degrees) Students may be familiar with the idea that a "360" represents a full rotation!
Now ask which way they would be facing if the turned another 360 degrees? (It would be facing the front again.) What if they turn 360 degrees 10 times (i.e. 3600 degrees)? (Still facing the front).
Using similar questions, help the students to realise that the total of the angles they turn modulo 360 gives the final result. For example, turning 3690 degrees to the right is the same as turning 90 degrees to the right (and the latter is a lot easier!) Doing rotations is just another kind of modulo arithmetic.
Doing these calculations in modulo 360 relates to programming in turtle-based languages such as Scratch and Logo, where sprites turn through angles. Turning left 90 degrees six times is the same as turning 540 degrees, but that puts the sprite in the same direction as it would be if it had turned 180 degrees. Likewise, turning 3600 (or 360, or 720) degrees is the same as turning 0 degrees! And 365 degrees is the same as 5 degrees. Turning -10 degrees is the same as 350 degrees.
Going to another extreme, ask the students to consider a clock with only two marks on it. What would they be? (They would be 0 and 1).
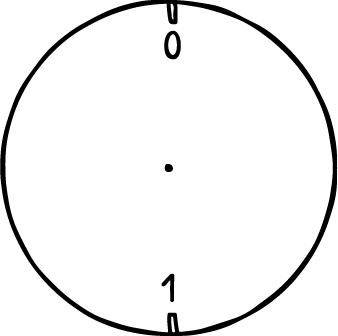
In this modulo 2 system, what is 1+1? (0).
What is 1+1+1? (1).
Count up through the numbers. For example, 4 is 4 ticks past 0, which gets you back to 0. Moving 5 ticks gets you to 1, 6 gets you back to 0. With some hints, students should realise that a number modulo 2 tells you if it is odd or even. This is used for the parity code! If you count black as 1 and white as 0, then each line with even parity adds up to 0 modulo 2. There's a parity error if it adds up to 1 modulo 2; and the extra bit that was added can be thought of as the value needed to make the line add up to 0, which is the same idea that is used for most of the other checksums, just with a different modulo!
Does the order matter?
Going back to the modulo 10 clock, ask students if the number 7+8 is different to the number 8+7. (They aren't, since they both are 15 ticks after 0). If necessary, use more examples, so that students recognise that this new way of adding isn't affected by the order.
Likewise, have them experiment with applying the mod function at each step of adding three numbers, compared with adding them first. For example, 7+8+6 gets to 1 on the clock. Now have them consider 7+8 (which gets to 5), and then add the 6 to it. It turns out that you can apply the modulo at each step, or just at the end; both give the same result.
This means that you can add numbers up quickly by grouping them. For example, suppose you're adding up: 3 + 7 + 2 + 9 + 1 + 3
You could work out the total (25), which is 5 in modulo 10. Or you could add up the digits in pairs. In this example, the first two digits add up to 0 mod 10: 3 + 7 = 0
This means that the 3 and the 7 cancel each other out - they won't affect the total. There's also a 9+1 in the sum, so that will also make no difference to the total. That leaves just 2 and 3 to add up, which come to 5 for the grand total.
By grouping numbers that add to 10 (or 20 etc.), you can usually add up several digits quite quickly in your head. This isn't useful on computers, but means you could possibly add up a product code checksum without even using pencil and paper!
Plugging it in
The "modulo" or "mod" function is easily tested in most programming languages.
In Scratch, you can just choose the "mod" block from the Operators, type in two numbers and double click it to see the result:
(37)mod(10) // 7
(-3)mod(10) // 7In several programming languages, the % sign is used to represent "modulo",
which is a very confusing choice!
You would type 37 % 10 to do the above calculation in Python, Java, C, C++,
C#, and JavaScript.
Some other languages use mod, including spreadsheets - for example, you
can type =mod(37,10) in a spreadsheet formula.
You could project a program onto the screen, and ask students to predict
the value when you type in two numbers.
For example, in Scratch you could put ((8)+(5))mod(12) into the
Scratch work area and double click it once students make their predictions.
In Python you would use (8+5)%12.
Now try 8+4 instead of 8+5. 8+12? 8+24? 8+25?
Fun facts
The months of the year are modulo 12; 4 months after November is March, 13 months after January is February, and so on (if you want to use the modulo function, you'd need to number the months from 0 to 11, which is a little unconventional).
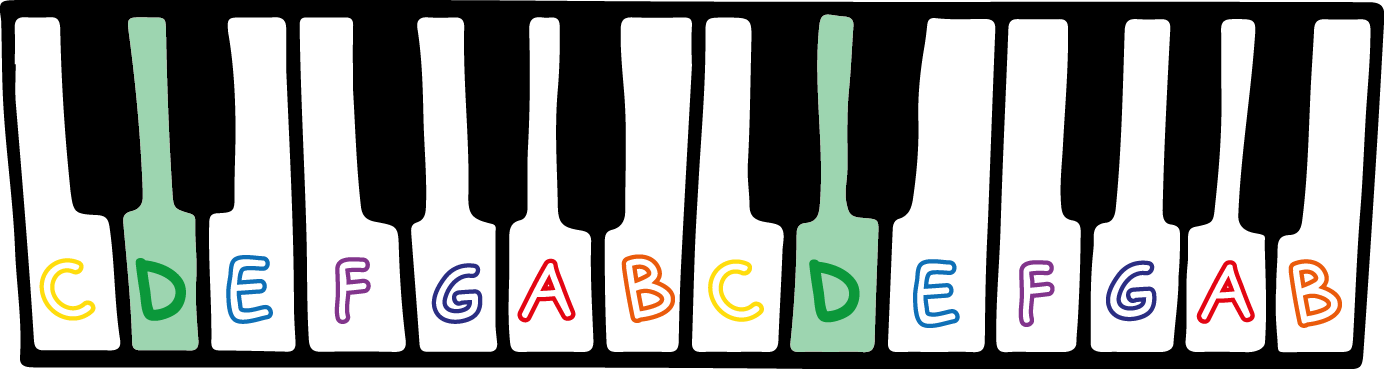
The naming of musical notes is modulo 7; if you start at the note "D" on a piano, and count up 7 white notes, you'll end up back on "D", which is the same note an octave higher. This raises the interesting fact that there are 7 different notes in an octave; it gets its name because if you count the notes at the start and end ("D" in this case, there are 8 notes).
Actually, there are really 12 different notes in an octave if you count the black keys (if you go 12 semitones up from the note "D", you'll end up at D again), so in this sense the 12 different notes on a piano are a lot like the 12 months or the 12 ticks on a 12-hour clock; but it would be really confusing if we referred to the notes as "January, February,...".
The cyclic number relationship comes up when playing notes in computer programs, which often use a digital representation of piano notes called MIDI (for example, these numbers are used in Scratch). In this system, middle C is note number 60, C# is 61, and D is 62. So an octave above 62 is 62+12 = 74. Every 12th number corresponds to the same note name. This will be explained in more detail in the activity on programming musical scales, which is under development.
Applying what we have just learnt
Mathematical concepts are part of our everyday life. Modular arithmetic (which uses the modulo function) is the formal term for clock arithmetic. As we expose students to the technical terms of things that we use every day, such as when learning to tell the time, the months of the year, and during our music lessons, the mathematical links become more obvious. The modulo function is also closely related to finding the remainder.
Lesson reflection
- Who were the students who were able to make the connections quickly?
- Were there any students who found this a logical way to calculate the remainder of a number?
- What surprised you and your students when learning about Modulo arithmetic?
Seeing the Computational Thinking connections
Throughout the lessons there are links to computational thinking. Below we've noted some general links that apply to this content.
Teaching computational thinking through CSUnplugged activities supports students to learn how to describe a problem, identify what are the important details they need to solve this problem, break it down into small logical steps so that they can then create a process which solves the problem, and then evaluate this process. These skills are transferable to any other curriculum area, but are particularly relevant to developing digital systems and solving problems using the capabilities of computers.
These Computational Thinking concepts are all connected to each other and support each other, but it’s important to note that not all aspects of Computational Thinking happen in every unit or lesson. We’ve highlighted the important connections for you to observe your students in action. For more background information on what our definition of Computational Thinking is see our notes about computational thinking.
This topic is primarily a maths topic, which supports later activities for computational thinking. The connections with Computational Thinking are therefore more indirect, since CT isn't the main purpose of the topic, and so we haven't provided the usual list of connections.
Nevertheless, there are some connections worth noting. One connection with computational thinking is an example of abstraction: sequences like "Monday, Tuesday, Wednesday..." or "January, February, March..." or "C, C#, D, D#, E, F..." can be represented by a cycle of numbers (0, 1, 2, 3...). There are also a lot of patterns for students to explore; for example, using modulo 10, the result is always the last digit, and using modulo 2 the pattern for ascending numbers is 0, 1, 0, 1, 0, 1..., that is, it alternates for even and odd numbers, and also corresponds to the right-hand bit of the binary representation.