Guess my number
This is similar to the game of 20 questions, but it is about guessing a number with the strict rule that you can only answer whether the secret number is greater than or equal to a guessed number.
What you need
- At least 2 people
- A pen or pencil
- Two or three pieces of paper
Skills needed
- Comparing numbers up to 100
Key question
How quickly can you find an answer just by asking questions that have a yes or no answer?
Activity steps

I’ve written a secret number on this paper, and you need to work out what it is. It’s between 1 and 100. Each time you tell me a number, I’ll tell you if my number is greater than or equal to your one. I won’t tell you if it’s equal - but you’ll still be able to work out my number!
Write a number on some paper, and fold it over so it can’t be seen. It can be any number from 1 to 100; in the example below the parent happens to have chosen 52 as the secret number.

What number do you want to guess first?
Write a "greater than or equals" symbol followed by their guess. (In the example, the child has guessed 50.)

(Depending on the number)
My secret number is not greater than or equal to your guess.
or
My secret number is greater than or equal to your guess.
Write a tick or cross depending on whether it is greater than or equal. Since 52 (the secret number) is greater than or equal to the guess (50), the presenter has written a cross.
Do not tell them if they have guessed your number! They will need to work out when they have enough information to know the number, so this is different to traditional versions of games like "20 guesses". The best guessing strategy is to start by guessing 50 (which the child happened to do in this case), but it’s fine if the child wants to use another approach - let them work it out for themselves!
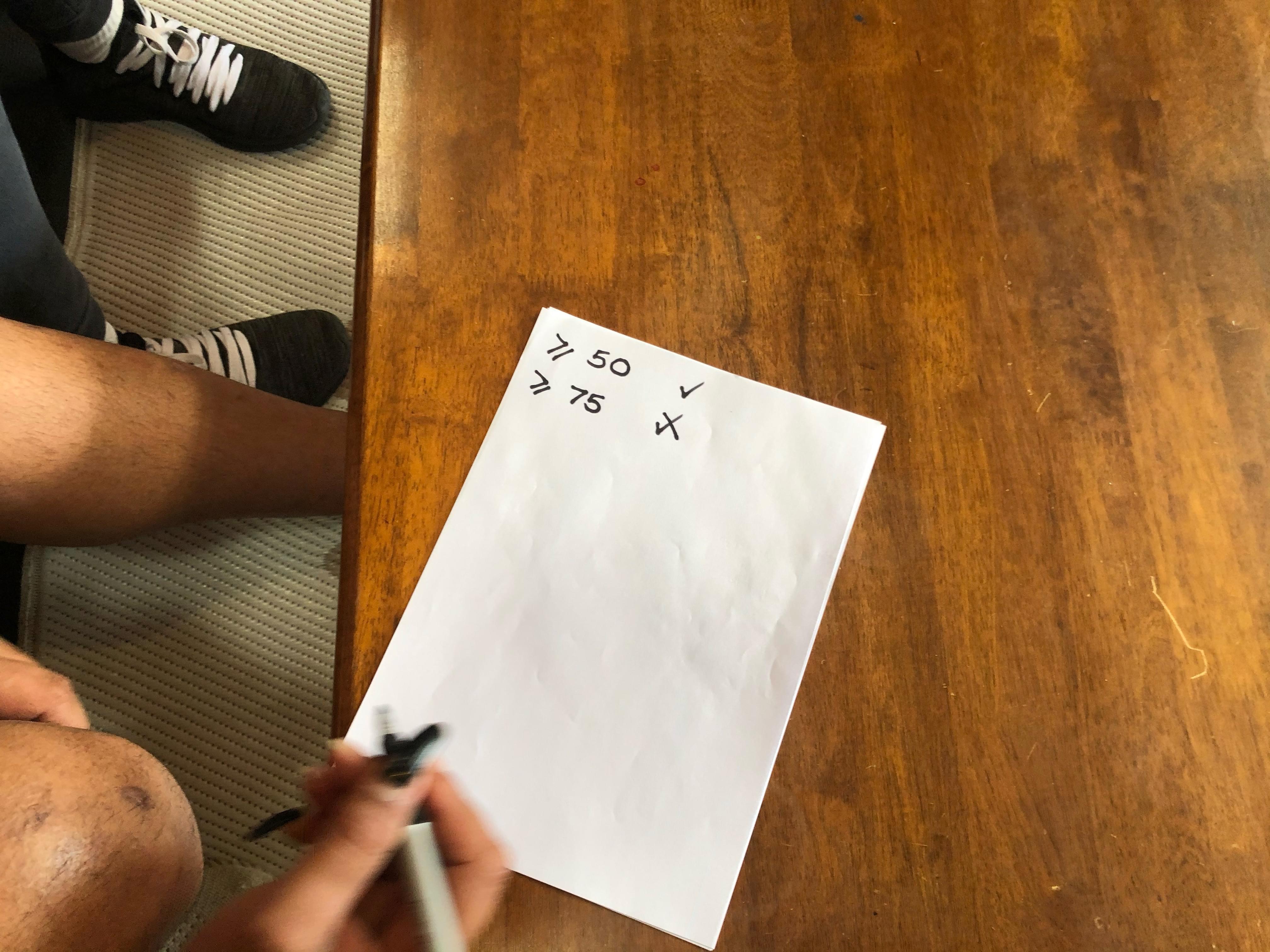
Which number do you want to guess next? Again, say one of these:
My secret number is not greater than or equal to your guess.
or
My secret number is greater than or equal to your guess.
In this case the child has guessed 75. The secret number isn’t greater than equal to 75, so the presenter has marked it with a cross.

This repeats until the child can guess the number.

In the example, the child happens to have named the secret number (52), but the presenter has only said that their guess is greater than or equal to the secret number.

As it happens, the child can deduce that the number must be 52 from the information available, since they found out earlier that it’s not greater than or equal to 53. It can take a bit of logic to work this out, but it’s always possible to narrow in on the number.

You can play this game a few times so that they can refine their strategy and develop their logical thinking to find the answer. After a while they may discover that it’s strategic to keep dividing the range in half.
Inside the computer
This activity touches on several key ideas in computing. One is that dividing big problems in half, then half again, and so on, makes them very small very quickly. With 100 possible values, only 7 questions are ever needed to narrow down to the secret value if you use the right strategy. In Arnold’s challenges students can experiment with guessing numbers from 1 to 1000 - it looks like it would be 10 times as hard, but it only needs three more questions! Every time the range doubles in size, you only need one more question to guess a number in the range. In fact, you could guess a number from 1 to a million using only 20 questions - it doesn’t take that long, although you might want to use a calculator to half the range each time. This approach to narrowing down towards a solution is behind some very fast computer algorithms.
Another idea in the activity is that you can achieve a lot with only "binary" yes/no decisions. You might think that you need to check if the final value is equal, but you can know for use only by using "greater than or equal". Decisions that have two outcomes (often referred to as true or false) are the basis of "Boolean logic", which is one of the key ideas used in the design of digital devices.
Arnold's challenges
Click here to view Arnold's challenges:
Arnold's Challenges

